Vectorisation
Contents
Vectorisation¶
Broadcasting¶
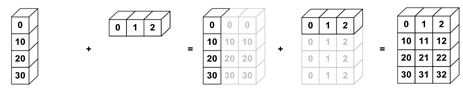
Broadcasting allows for operations with different shaped arrays.
It’s implemented in many libraries, such as NumPy and xarray.
import numpy as np
nums_col = np.array([0, 10, 20, 30]).reshape(4, 1)
nums_col
array([[ 0],
[10],
[20],
[30]])
nums_row = np.array([0, 1, 2])
nums_row
array([0, 1, 2])
nums_col + nums_row
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
import xarray as xr
nums_col = xr.DataArray([0, 10, 20, 30], [('col', [0, 10, 20, 30])])
nums_col
<xarray.DataArray (col: 4)> array([ 0, 10, 20, 30]) Coordinates: * col (col) int64 0 10 20 30
nums_row = xr.DataArray([0, 1, 2], [('row', [0, 1, 2])])
nums_row
<xarray.DataArray (row: 3)> array([0, 1, 2]) Coordinates: * row (row) int64 0 1 2
nums_col + nums_row
<xarray.DataArray (col: 4, row: 3)>
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
Coordinates:
* col (col) int64 0 10 20 30
* row (row) int64 0 1 2Vectorisation¶
Vectorisation allows the code to operate on multiple array elements at once, rather than looping through them one at a time.
NumPy has many functions already vectorised for you, which have been optimised in C (i.e., they’ve been statically typed and compiled).
These are known as the universal functions (ufuncs).
There are many operations available, for maths (e.g., add and subtract), trigonometric (e.g., sin and cos), comparison (e.g., greater and less), and floating (e.g., isnan)
For example, instead of using +, you can use the equivalent ufunc np.add:
nums = np.arange(1_000_000)
%%timeit
[num + 2 for num in nums]
209 ms ± 596 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
%%timeit
nums + 2 # adds 2 to every element by overloading the + (similar to broadcasting)
693 µs ± 7.8 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
%%timeit
np.add(nums, 2)
689 µs ± 9.91 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Question
If something doesn’t vary for a given loop, should it be inside or outside of that loop?
Solution
Loop-invariants should be move outside of loops.
This is because loops are slow in Python (CPython, default interpreter).
Loops are slow because loops type−check and dispatch functions per cycle.
Try to avoid them where can (e.g., using NumPy ufuncs, aggregations, broadcasting, etc.).
Create your own ufunc¶
You can vectorise any arbitrary Python function to a NumPy ufunc using np.vectorize.
Don’t worry about what this function does, just focus on the vectorisation bit.
import math
SQRT_2PI = np.float32((2.0 * math.pi)**0.5)
x = np.random.uniform(-3.0, 3.0, size=1_000_000)
mean = 0.0
sigma = 1.0
def my_function(x, mean, sigma):
'''Compute the value of a Gaussian probability density function at x with given mean and sigma.'''
return math.exp(-0.5 * ((x - mean) / sigma)**2.0) / (sigma * SQRT_2PI)
vectorized_function = np.vectorize(my_function)
%%timeit
vectorized_function(x, mean, sigma)
2.24 s ± 6.94 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Question
Can you run the unvectorised my_function directly on the same inputs (i.e., all of x)?
Solution
No, a TypeError is returned.
As the function has not yet been vectorised, it cannot operate across arrays with more than 1 element.
To check that it does work for 1 element, you could try: my_function(x[0], mean, sigma).
Exercises¶
Exercise 1
What is broadcasting?
Solution
Broadcasting allows for operations with different shaped arrays.
Exercise 2
What is vectorisation?
Solution
Vectorisation allows the code to operate on multiple array elements at once, rather than looping through them one at a time.
Exercise 3
How would you replace the compute_reciprocals function below with a vectorised version?
def compute_reciprocals(array):
"""
Divides 1 by an array of values.
"""
output = np.empty(len(array))
for i in range(len(array)):
output[i] = 1.0 / array[i]
return output
big_array = np.random.randint(1, 100, size=1_000_000)
%timeit compute_reciprocals(big_array)
1.87 s ± 2.38 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Solution
You can either use the np.divide ufunc as follows:
%timeit np.divide(1.0, big_array)
1.29 ms ± 124 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Or you could just use /, which works on every element by overloading the operator (similar to broadcasting):
%timeit (1.0 / big_array)
1.19 ms ± 103 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Exercise 4
Create your own vectorised ufunc that calculates the cube root of an array over all elements.
Hint
Here is an unvectorised version (i.e., it has a for loop):
def my_cube_root(array):
output = np.empty(len(array))
for i in range(len(array)):
output[i] = array[i] ** (1 / 3)
return output
%timeit my_cube_root(big_array)
1.77 s ± 152 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Solution
Option 1:
You could use the np.vectorize decorator:
import math
from numpy import vectorize
@vectorize
def my_cube_root(array):
return math.pow(array, 1/3)
%timeit my_cube_root(big_array)
213 ms ± 33.1 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Option 2:
You could overload the ** and / symbols:
def my_cube_root(array):
return array ** (1 / 3)
%timeit my_cube_root(big_array)
36 ms ± 864 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Option 3:
You could use the optimised ufuncs from NumPy or SciPy (recommended):
%timeit np.cbrt(big_array)
13.9 ms ± 1.51 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
from scipy.special import cbrt
%timeit cbrt(big_array)
18.9 ms ± 1.9 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
Key Points¶
Important
Take advantage of broadcasting for different shaped arrays.
Use vectorised functions where you can e.g., NumPy ufuncs.
